




L'introduction de modèles statistiques inspirés de la physique des phénomènes sous-jacents et numériquement efficaces est d'un intérêt croissant pour la prédiction de processus spatio-temporels en sciences environnementales. Les grands jeux de données spatio-temporelles nécessitent de nouvelles méthodes numériques efficaces. L'approche par Equations aux Dérivées Partielles Stochastiques (EDPS) s'est avérée efficace pour l'estimation et la prédiction dans un contexte spatial. Nous présentons ici une EDPS d'advection-diffusion avec une dérivée de premier ordre en temps qui définit une grande classe de modèles spatio-temporels non séparables. On construit une approximation de la solution de l'EDPS par un champ aléatoire Markovien Gaussien en discrétisant la dérivée temporelle par la méthode des différences finies (Euler implicite) et en résolvant l'EDPS spatiale par la méthode des éléments finis (Galerkin continu) à chaque pas de temps. La technique de stabilisation "Streamline Diffusion" est introduite lorsque le terme d'advection domine la diffusion. Des méthodes de calcul efficaces sont proposées pour estimer les paramètres de l'EDPS et pour prédire le champ spatio-temporel par krigeage, ainsi que pour effectuer des simulations conditionnelles. L'approche est appliquée à des jeux de données de rayonnement solaire et de vitesse du vent. Ses avantages et ses limites sont examinées, et de nouvelles perspectives de travail sont envisagées, notamment afin de proposer une extension dans un cadre non stationnaire. On présente également un travail portant sur la généralisation non séparable de la classe de Gneiting des fonctions de covariance spatio-temporelles multivariées. Le principal potentiel de l'approche est la possibilité d'obtenir des modèles entièrement non séparables dans un cadre multivarié, et les avantages sont illustrés sur un ensemble de données météorologiques trivariées. De plus, on propose une analyse de méthodes d'estimation et de prédiction approximées pour les données spatiales et spatio-temporelles, motivée par l'objectif de parvenir à un compromis entre l'efficacité statistique et la complexité computationnelle. Ces méthodes se sont avérées efficaces pour l'estimation des paramètres et la prédiction dans le contexte de la "Compétition de statistiques spatiales pour les grands jeux de données" organisée par la King Abdullah University of Science and Technology (KAUST) en 2021 et 2022. Enfin, d'autres pistes de recherche sont envisagées et examinées.
In the task of predicting spatio-temporal fields in environmental science using statistical methods, introducing statistical models inspired by the physics of the underlying phenomena that are numerically efficient is of growing interest. Large space-time datasets call for new numerical methods to efficiently process them. The Stochastic Partial Differential Equation (SPDE) approach has proven to be effective for the estimation and the prediction in a spatial context. We present here the unsteady advection-diffusion SPDE which defines a large class of nonseparable spatio-temporal models. A Gaussian Markov random field approximation of the solution to the SPDE is built by discretizing the temporal derivative with a finite difference method (implicit Euler) and by solving the spatial SPDE with a finite element method (continuous Galerkin) at each time step. The Streamline Diffusion stabilization technique is introduced when the advection term dominates the diffusion. Computationally efficient methods are proposed to estimate the parameters of the SPDE and to predict the spatio-temporal field by kriging, as well as to perform conditional simulations. The approach is applied to solar radiation and wind speed datasets. Its advantages and limitations are discussed, and new perspectives for future work are envisaged, especially involving a nonstationary extension of the approach. As a further contribution of the PhD, the nonseparable generalization of the Gneiting class of multivariate space-time covariance functions is presented. The main potential of the approach is the possibility to obtain entirely nonseparable models in a multivariate setting, and this advantage is shown on a weather trivariate dataset. Finally, a review of some methods for approximate estimation and prediction for spatial and spatio-temporal data is proposed, motivated by the objective of reaching a trade-off between statistical efficiency and computational complexity. These methods proved to be effective for parameter estimation and prediction in the context of the "Spatial Statistics Competition for Large Datasets" organized by the King Abdullah University of Science and Technology (KAUST) in 2021 and 2022. Lastly, possible further research directions are discussed.
> plus d'informations sur le site dédié

Ecole
240 ans de recherche et de formation
Vidéo : 240ans de recherche…
> En savoir +

Formation
Samuel Forest, élu membre de l’Académie des…
Samuel Forest lors de sa réception à…
> En savoir +

Formation
Mines Paris plébiscitée par ses étudiantes
Mines Paris - PSL, une école qui répond…
> En savoir +

Formation
Corentin Gombert, prix de thèse de l’ARIMHE
Corentin Gombert, doctorant au CGS Mines Paris - PSL, lors de…
> En savoir +
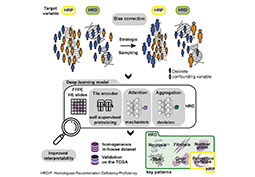
Formation
L'analyse d'images pour une médecine personnalisée du…
L'interprétation des prédictions des…
> En savoir +

Formation
Femmes de science
Chercheuses confirmées, doctorantes, élèves ou alumni,…
> En savoir +
Voir l'agenda des formations et autres actualités
Consultez régulièrement les offres de formation