




La théorie spatiale des valeurs extrêmes permet de modéliser et prédire la fréquence d'évènements extrêmes ayant une étendue spatiale comme, par exemple, des pluies ou des températures extrêmes, ou encore de fortes concentrations de pollution atmosphérique. Elle s'adapte bien aux données temporelles, lorsque le phénomène spatial étudié est observé plusieurs fois dans le temps. Cependant, nous n'avons parfois pas accès à de telles données: seulement un ou quelques enregistrements sont disponibles. C'est le cas, par exemple, des études sur l'estimation des ressources minières ou sur l'évaluation de la pollution des sols et plus généralement de toute recherche dont l'objet d'étude varie très peu au cours du temps ou pour lequel le coût d'échantillonnage est trop élevé. Ce cas de figure est très peu abordé par la communauté des extrêmes. Au contraire, c'est un cadre d'analyse auquel la Géostatistique s'intéresse particulièrement. Les travaux réalisés au cours de cette thèse ont pour objectif d'établir des connexions mathématiques entre ces deux disciplines afin de mieux appréhender les évènements extrêmes, lorsque le phénomène spatial sous-jacent n'est observé qu'une seule fois. Nous nous intéressons, dans un premier temps, au concept de portée intégrale. Intrinsèquement lié aux propriétés d'ergodicité et de mélange, ce paramètre issu de la théorie géostatistique caractérise les fluctuations statistiques, à large échelle, d'un champ aléatoire stationnaire. Lorsque ce dernier est un champ max-stable, nous montrons que sa fonction coefficient extrémal (ECF) est fortement liée à la portée intégrale du champ des excès, au dessus d'un certain seuil, correspondant. Cette approche permet de retrouver et de compléter des résultats précédemment établis dans un contexte de risque spatialisé. Elle met également en évidence une nouvelle expression de la fonction coefficient extrémal qui dépend du variogramme du champ des excès. À partir de cette formule, nous proposons un nouvel estimateur non-paramétrique de l'ECF. Ses propriétés asymptotiques sont établies lorsqu'il est évalué à partir d'une unique réalisation, partiellement observée, d'un champ stationnaire max-stable. En particulier, lorsque le nombre d'observations se densifie en même temps que le champ d'observation grandit, et sous certaines hypothèses concernant la portée intégrale susmentionnée, nous montrons qu'il est consistent et asymptotiquement normal. Il est donc pertinent d'utiliser les outils géostatistiques pour enrichir l'analyse des valeurs extrêmes. Finalement, nous développons un nouvel algorithme permettant de simuler, en continu, des processus aléatoires tempête pour lesquels la fonction de forme est déterministe. Il se distingue donc de la plupart des algorithmes existants qui s'utilisent exclusivement lorsque le domaine de simulation est composé d'un nombre fini de points. À cet égard, il permet d'étudier plus facilement la géométrie des réalisations de tels processus. Cela est particulièrement intéressant quand la caractéristique géométrique étudiée mêle différentes échelles d'observation.
Spatial extreme value theory helps model and predict the frequency of extreme events in a spatial context like, for instance, extreme precipitations, extreme temperatures or high concentrations of pollution in the air. It is well adapted to time series, when the spatial object under study is observed through time. However, in some cases, such types of data cannot be accessed: only one or just a few records are made available. This is the case, for instance, in mining resources estimation, soil contamination evaluation or any other applications where the phenomenon of interest either varies too slowly across time to hope for a decent time series, or is too expensive to sample from. This situation is rarely addressed in the spatial extremes community, contrary to Geostatistics, which typically deals with such issues. The aim of this thesis is to make some connections between both disciplines, in order to better handle the study of spatial extreme events when having only one set of spatial observations. We first focus on the concept of integral range. Intimately related to the ergodic and mixing properties, it is a geostatistical parameter that characterizes the statistical fluctuations of a stationary random field at large scale. When the latter is max-stable, we show that its extremal coefficient function (ECF) is closely related to the integral range of the corresponding exceedance field above a threshold. This approach allows to retrieve and complete previous results established in a spatial risk context. It also has the advantage of revealing a new expression for the extremal coefficient function that depends on the variogram of the exceedance field. From this, we move to proposing a new nonparametric estimator of the ECF. Its asymptotic properties are derived when it is computed from a single and partially observed realization of a stationary max-stable random field. Specifically, considering both infill and increasing domain asymptotics, and under some assumptions on the aforementioned integral range, we prove that it is consistent and asymptotically normal. This illustrates the relevance of geostatistical tools for enriching extreme value analysis. Finally, we develop a novel algorithm to perform exact simulations in a continuous domain of storm processes with deterministic shape function. It distinguishes itself from most existing algorithms, which apply to simulation domains made of a finite number of points. In this regard, it allows for easier investigation about the geometry of realizations of such processes. This is of particular interest when the geometric feature under study involves different scales of observation.
Titre anglais : Spatial extremes with a single realization: a geostatistical point of view
Date de soutenance : lundi 5 octobre 2020 à 14h00
Adresse de soutenance : MINES ParisTech 60 Boulevard Saint-Michel 75006 Paris - L109
Directeurs de thèse : Hans WACKERNAGEL, Emilie CHAUTRU

Ecole
240 ans de recherche et de formation
Vidéo : 240ans de recherche…
> En savoir +

Formation
Samuel Forest, élu membre de l’Académie des…
Samuel Forest lors de sa réception à…
> En savoir +

Formation
Mines Paris plébiscitée par ses étudiantes
Mines Paris - PSL, une école qui répond…
> En savoir +

Formation
Corentin Gombert, prix de thèse de l’ARIMHE
Corentin Gombert, doctorant au CGS Mines Paris - PSL, lors de…
> En savoir +
Formation
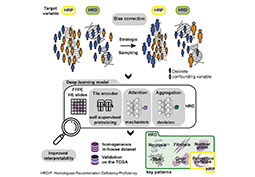
L'analyse d'images pour une médecine personnalisée du…
L'interprétation des prédictions des…
> En savoir +

Formation
Femmes de science
Chercheuses confirmées, doctorantes, élèves ou alumni,…
> En savoir +
Voir l'agenda des formations et autres actualités
Consultez régulièrement les offres de formation